Embark on a geometric journey with Kuta parallel and perpendicular lines, where we delve into the intricacies of these fundamental concepts that shape our world. From everyday observations to intricate theorems, this exploration unravels the fascinating interplay of parallel and perpendicular lines.
Delve into the defining properties and methods for identifying parallel and perpendicular lines. Discover the power of geometric tools and theorems in solving geometry problems, and witness the practical applications of these concepts in the real world.
Kuta Parallel and Perpendicular Lines

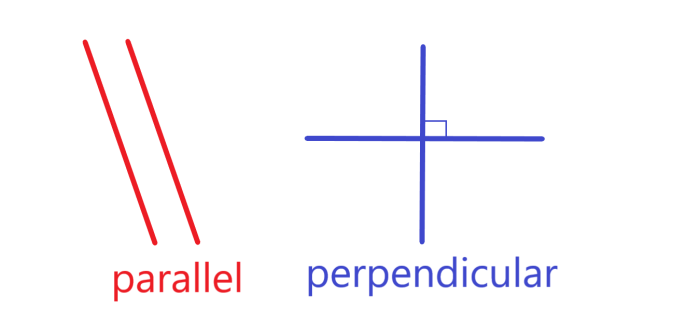
Parallel lines are lines that never intersect, while perpendicular lines are lines that intersect at a right angle (90 degrees). Parallel lines are often used to create the illusion of depth or perspective in drawings and paintings, while perpendicular lines are often used to create the illusion of height or stability.
Examples of Parallel and Perpendicular Lines in Everyday Life
Examples of parallel lines in everyday life include the sides of a rectangular picture frame, the rails of a railroad track, and the lines on a sheet of graph paper. Examples of perpendicular lines in everyday life include the sides of a square or rectangle, the legs of a chair, and the lines that form the corners of a building.
Identifying Parallel and Perpendicular Lines

Identifying parallel and perpendicular lines is crucial in geometry. Understanding their properties and the methods to identify them using geometric tools is essential for solving geometric problems accurately.
Properties of Parallel and Perpendicular Lines
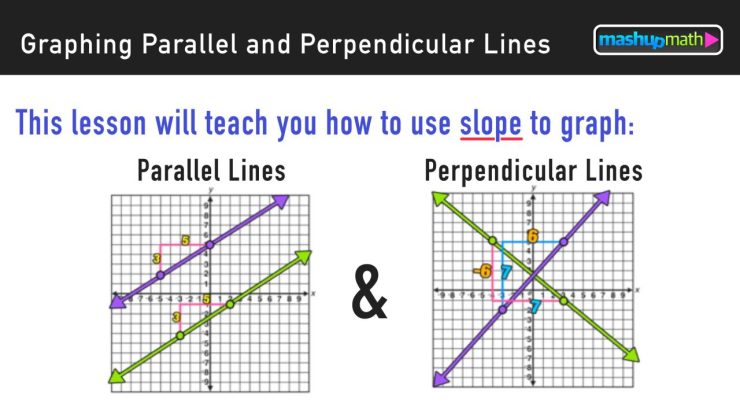
- Parallel lines are lines that never intersect, no matter how far they are extended.
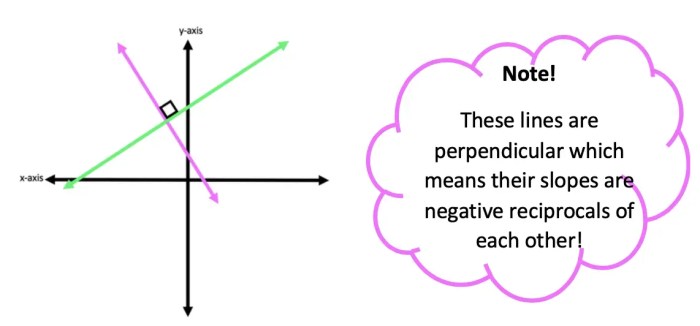
- Perpendicular lines are lines that intersect at a right angle (90 degrees).
Methods for Identifying Parallel and Perpendicular Lines, Kuta parallel and perpendicular lines
Using a Protractor
A protractor is a tool used to measure angles. To identify parallel lines using a protractor, place the protractor on the lines and measure the angle between them. If the angle is 0 degrees, the lines are parallel. If the angle is 90 degrees, the lines are perpendicular.
Using a Compass and Straightedge
A compass and straightedge can also be used to identify parallel and perpendicular lines. To identify parallel lines, use the compass to draw an arc that intersects both lines. Then, use the straightedge to draw a line parallel to the first line that passes through the point of intersection on the second line.
The two lines will be parallel.
To identify perpendicular lines, use the compass to draw an arc that intersects both lines. Then, use the straightedge to draw a line perpendicular to the first line that passes through the point of intersection on the second line. The two lines will be perpendicular.
Using the Properties of Parallel and Perpendicular Lines
In addition to using geometric tools, the properties of parallel and perpendicular lines can also be used to identify them. For example, if two lines are parallel to a third line, they are parallel to each other. If two lines are perpendicular to a third line, they are perpendicular to each other.
Theorems and Applications: Kuta Parallel And Perpendicular Lines
Theorems related to parallel and perpendicular lines form the cornerstone of Euclidean geometry. These theorems provide a framework for understanding the relationships between lines and angles, enabling the development of geometric proofs and the solution of geometric problems.
Theorems
One of the fundamental theorems in this area is the Parallel Postulate, which states that through a point not on a given line, there is exactly one line parallel to the given line.
Another important theorem is the Perpendicular Bisector Theorem, which states that the perpendicular bisector of a line segment is the set of all points equidistant from the endpoints of the line segment.
Applications
These theorems have numerous applications in solving geometry problems. For example, the Parallel Postulate is used to prove that the sum of the interior angles of a triangle is 180 degrees.
The Perpendicular Bisector Theorem is used to construct perpendicular bisectors, which are essential for finding the centers of circles and for solving problems involving the distance between points and lines.
Real-World Applications
Understanding parallel and perpendicular lines is essential in various real-world applications. For instance, architects use these concepts to design buildings and bridges, ensuring structural stability and aesthetic appeal.
In engineering, parallel lines are used to create parallel circuits, which are important for controlling the flow of electricity. Perpendicular lines are used to create perpendicular joints, which are essential for transferring loads in structures.
Geometric Constructions
Geometric constructions involving parallel and perpendicular lines are fundamental in geometry. These constructions are essential for creating accurate and precise geometric figures.
Constructing Parallel Lines
To construct parallel lines using a compass and straightedge:
- Draw a line segment AB.
- Place the compass on point A and draw an arc that intersects AB at C.
- Without changing the compass width, place the compass on point B and draw an arc that intersects the previous arc at D.
- Draw a line through points C and D. This line will be parallel to AB.
Constructing Perpendicular Lines
To construct perpendicular lines using a compass and straightedge:
- Draw a line segment AB.
- Place the compass on point A and draw an arc that intersects AB at C.
- Without changing the compass width, place the compass on point B and draw an arc that intersects the previous arc at D.
- Draw a line through points C and D. This line will be perpendicular to AB.
General Inquiries
What are the key characteristics of parallel lines?
Parallel lines are lines that never intersect, no matter how far they are extended.
How can you identify perpendicular lines using a protractor?
To identify perpendicular lines using a protractor, measure the angle between the two lines. If the angle measures 90 degrees, the lines are perpendicular.
What is the Pythagorean theorem and how does it relate to perpendicular lines?
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem can be used to determine if two lines are perpendicular.